「平均値の定理」は知ってはいても、入試問題で使いこなすのは意外と難しいですよね
実は平均値の定理は３つの使い所を抑えておくだけで、色んな問題で活用することができるんです！
今回はそんな平均値の定理の活用法について解説し，千葉大と名古屋大の過去問を実際に解いてみます！
今回のポイント
今回抑えて欲しい内容は以下の通りです
- 平均値の定理の活用法について知る
- 平均値の定理の３つの使い所を抑える
- 実際に平均値の定理を使って入試問題を解けるようにする
では説明していきます！
平均値の定理と活用法
まず平均値の定理とは
「関数 \(f(x)\) が \(a \leq x \leq b\) で連続かつ \(a<x<b\) で微分可能であるとき，
\begin{align}
\frac{f(b)-f(a)}{b-a}=f'(c) \label{eq1}
\end{align}
かつ
\begin{align}
a<c<b \label{eq2}
\end{align}
を満たす実数 \(c\) が少なくとも１つ存在する」
という定理です
ここでもし \(f(x)\) の一回微分 \(f'(x)\) が単調増加のグラフだとすると， \(f'(a)<f'(c)<f'(b)\) となるので\(f'(c)\) を消去すると，
\begin{align}
\quad&(b-a) f'(a) \\
<&f(b)-f(a) \\
<&(b-a)f'(b) \label{eq3}
\end{align}
が成り立ちます
そしてさらに \(a=n\) ， \(b=n+1\) とすると，
\begin{align}
\quad&f'(n) \\
<& f(n+1)-f(n) \\
<& f'(n+1) \label{eq4}
\end{align}
となります
この式はあまり習わないですが，不等式の証明はもちろん， \(f(n+1)-f(n)\) の極限を聞かれたときの「はさみうちの原理」にも活用可能なので非常に大切なんです！
(ちなみに \(f'(x)\) が単調減少のときは不等号の向きが逆になります)
つまり平均値の定理はここまで変形して初めて様々な入試問題で活用することができます！
本当に重要なので、念の為ここまでの説明をまとめておくと
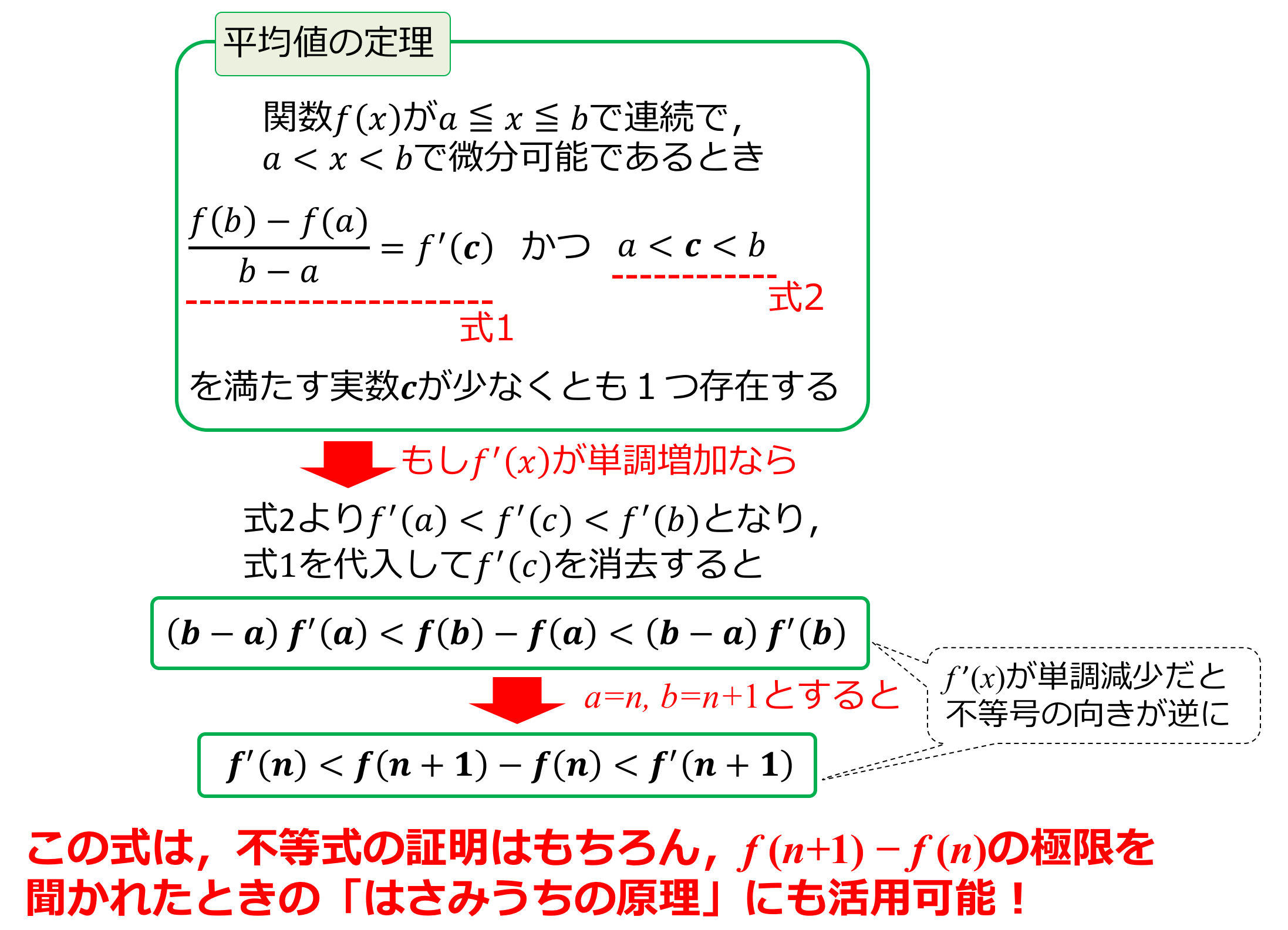
となります
では次に実際にどういった問題で平均値の定理を使うことが出来るのか確認していきましょう
平均値の定理の使いどころ
さきほどの説明から平均値の定理の使い所は以下の３つを満たしている問題です
① 不等式の証明 or 極限(はさみうち)
② \(f(n+1)-f(n)\) のような差分の形
③ \(f'(x)\) が単調増加 or 単調減少
具体的には以下のような入試問題です
この千葉大の問題は不等式の証明問題であり，与式を変形すると
\begin{align} n\{\log{(n+1)}-\log{n}\}-\log(n+1)<0 \end{align}
となって\(\log{(n+1)}-\log{n}\) という差分の形が登場します
そして\(\displaystyle (\log{x})'=\frac{1}{x}\) は単調減少のグラフになることから，平均値の定理の使い所①，②，③を全て満たすので「平均値の定理を使おう！」となります
もう一つ例をあげましょう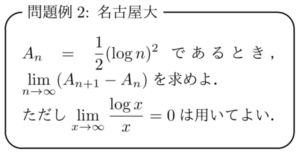
この名古屋大の問題は，極限問題かつ \(A_{n+1}-A_n\) という差分の形です．
そして \(\displaystyle f(x)=\frac{1}{2}(\log x)^2\) とおくと， \(\displaystyle f'(x)=\frac{\log{x}}{x}\) ， \(\displaystyle f''(x)=\frac{1-\log{x}}{x^2}\) となり，
\(x\) が十分大きい値では \(f''(x)<0\) となって \(f'(x)\) は単調減少すると分かるので「平均値の定理を使おう！」となります
では次にこれらの問題で実際に問題を解いていくにはどうすればよいか確認しましょう
入試問題の解き方
さきほどの千葉大と名古屋大の問題を平均値の定理を使って最後まで解いていきます
千葉大の問題
千葉大の解答
まず与式を変形すると
\begin{align}
\quad&\frac{\log{n}}{n-1}>\frac{\log{(n+1)}}{n} \nonumber \\
\Leftrightarrow&n\{\log{(n+1)}-\log{n}\}-\log(n+1)<0 \label{tiba1}
\end{align}
となるので，こちらを示します
ここで \(f(x)=\log{x}\) とすると，2以上の整数 \(n\) に対し， \(f(x)\) は \(n\leq{x}\leq{n+1}\) で連続， \(n<x<n+1\) で微分可能なので，平均値の定理より，
\begin{align}
\frac{f(n+1)-f(n)}{(n+1)-n}=f'(c_n) \nonumber
\end{align}
かつ
\begin{align}
n<c_n<n+1 \nonumber
\end{align}
を満たす実数 \(c_n\) が少なくとも１つ存在します
そして \(\displaystyle f'(x)=\frac{1}{x}\) は単調減少のグラフなので
\begin{align}
\quad& n<c_n \\ \nonumber
\Leftrightarrow& f'(c_n)<f'(n) \\ \nonumber
\Leftrightarrow& \log{(n+1)}-\log{n}<\frac{1}{n} \nonumber
\end{align}
となります
\(n\geq 2 \)を念頭に置きつつ、さらに変形すると
\begin{align}
\require{physics}
\quad& n\{\log{(n+1)}-\log{n}\}-\log(n+1) \\
< & n\times\frac{1}{n}-\log(n+1) \nonumber \\
=& 1-\log(n+1) \nonumber \\
=& \log{e}-\log(n+1)<0 \hspace{2mm} \nonumber
\end{align}
となり与式が成立すると分かります
名古屋大の問題
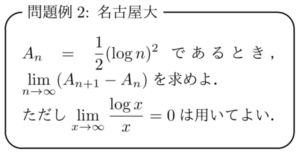
名古屋大の解答
\(\displaystyle f(x)=\frac{1}{2}(\log x)^2\) とすると，各自然数 \(n\) に対し， \(f(x)\) は \(n\leq{x}\leq{n+1}\) で連続， \(n<x<n+1\) で微分可能なので，平均値の定理より，
\begin{align}
\frac{f(n+1)-f(n)}{(n+1)-n}=f'(c_n) \nonumber
\end{align}
かつ
\begin{align}
n<c_n<n+1 \nonumber
\end{align}
を満たす実数 \(c_n\) が少なくとも１つ存在します
ここで \(n\) が十分大のとき，
\(n\leq{x}\leq{n+1}\) で
\begin{align}
f'(x)&=\frac{\log{x}}{x}\nonumber \\
f''(x)&=\frac{1-\log{x}}{x^2}<0 \nonumber
\end{align}
より， \(f'(x)\) は単調減少するので，
\begin{align}
\quad& n<c_n<n+1 \nonumber \\
\Leftrightarrow& f'(n+1)<f'(c_n)<f'(n) \nonumber \\
\Leftrightarrow&\frac{\log(n+1)}{n+1}<A_{n+1}-A_n<\frac{\log{n}}{n} \nonumber
\end{align}
が成り立ちます
ここで
\begin{align}
\quad&\lim_{n\to{\infty}} \frac{\log(n+1)}{n+1}=0 \\
\quad&\lim_{n\to{\infty}} \frac{\log{n}}{n}=0\nonumber
\end{align}
なので，はさみうちの原理より，
\begin{align}
\lim_{n\to{\infty}} (A_{n+1}-A_n)=0\nonumber
\end{align}
と分かります