メネラウスの定理は誰しも一度は習うもののいざ使うとなると難しいですよね
またあまり知られていないのですが,以下のようにメネラウスは注目している直線と三角形が交わらない場合でも成立します
(黄チャートp347重要例題74でも登場)
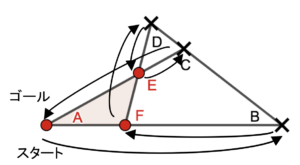
\begin{align}
\frac{\mathrm{AB}}{\mathrm{BF}}\times\frac{\mathrm{FD}}{\mathrm{DE}}\times \frac{\mathrm{EC}}{\mathrm{CA}} = 1
\end{align}
今回はそんなメネラウスの使い方を全パターンとともに解説します
●と×をつけて交互に辿るようにすると,簡単に使いこなせるようになります!
今回のポイント
今回抑えて欲しい内容は以下の通りです
- メネラウスの定理の使い方をマスターする
- 全4パターンを使いこなせるようにする
では説明していきます!
メネラウスの定理の使い方
メネラウスの定理を使うときは3つのステップで考えます
ステップ1:キツネの形に注目
ステップ1ではまず以下のような図形に注目します
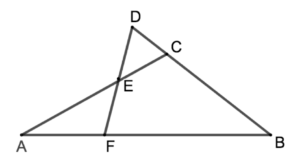
三角形ABCと三角形BDFを組み合わせような形になっていますね
僕はこれを「キツネの形」と呼んでいます
メネラウスの定理を使いたいときはまずキツネの形を見つけましょう!
ステップ2:三角形に注目
ステップ2では先ほどの「キツネの形」に含まれている三角形に注目します
さきほどの図でいうと三角形BDF,三角形ABC,三角形CDE,三角形AEF,の4つのうちのどれかに注目します
そしてその三角形の各頂点に●,それ以外の点に☓をつけます
試しに三角形BDFに注目すると
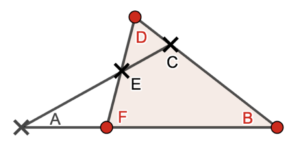
のようになります
ステップ3:各頂点を●と☓交互にたどる
最後にステップ3では「キツネの形」内の好きな点から各頂点を●と☓交互にたどって一周し,辿った頂点順に立式します
さきほどの図で試しに頂点Bから上に向かってスタートすると
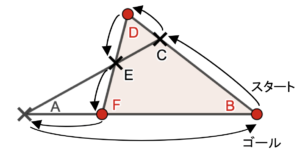
のように,辿った頂点の順に合わせて式を立てると
\begin{align}
\frac{\mathrm{BC}}{\mathrm{CD}}\times\frac{\mathrm{DE}}{\mathrm{EF}}\times \frac{\mathrm{FA}}{\mathrm{AB}} = 1
\end{align}
のようになります
メネラウスの全4パターン
先ほどのステップ2では三角形に注目しましたが,「キツネの形」には4つの三角形が含まれているため,どの三角形を選ぶかで,ステップ3の立式が変わってきます
つまりメネラウスの定理は全部で4パターンあることになります
その4パターンについて以下にまとめておきます
特に後半の2つを知らない人は多いと思うので,是非確認しておいてください!
① 三角形BDFに注目
三角形BDFに注目し頂点Bから上に向かってスタートすると
 となり,たどった頂点順に式をたてると
となり,たどった頂点順に式をたてると
\begin{align}
\frac{\mathrm{BC}}{\mathrm{CD}}\times\frac{\mathrm{DE}}{\mathrm{EF}}\times \frac{\mathrm{FA}}{\mathrm{AB}} = 1
\end{align}
となります
② 三角形ABCに注目
三角形ABCに注目し頂点Aから右に向かってスタートすると
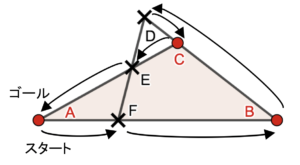
となり,たどった頂点順に式をたてると
\begin{align}
\frac{\mathrm{AF}}{\mathrm{FB}}\times\frac{\mathrm{BD}}{\mathrm{DC}}\times \frac{\mathrm{CE}}{\mathrm{EA}} = 1
\end{align}
となります
③ 三角形CDEに注目
三角形CDEに注目し頂点Dから下に向かってスタートすると
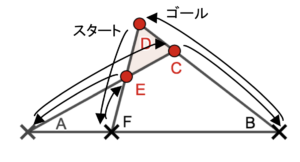
となり,たどった頂点順に式をたてると
\begin{align}
\frac{\mathrm{DF}}{\mathrm{FE}}\times\frac{\mathrm{EA}}{\mathrm{AC}}\times \frac{\mathrm{CB}}{\mathrm{BD}} = 1
\end{align}
となります
④ 三角形AEFに注目
三角形AEFに注目し頂点Aから右に向かってスタートすると

となり,たどった頂点順に式をたてると
\begin{align}
\frac{\mathrm{AB}}{\mathrm{BF}}\times\frac{\mathrm{FD}}{\mathrm{DE}}\times \frac{\mathrm{EC}}{\mathrm{CA}} = 1
\end{align}
となります