外積の定義と分かりやすい計算法

外積は黄チャート数ⅡBのp418でも触れられていますが、正しく使いこなせると計算時間が大幅に短縮できかなり便利な手法です
今回はそんな外積について基礎から説明します
特に外積の計算方法は他のどのサイトよりも分かりやすいと思います

今回のポイント
外積とは
外積の計算方法と覚え方

今回のポイント

今回抑えて欲しいポイントは以下の2つです

外積とは何かを知る
外積の計算方法をマスターする

では説明していきます！

外積とは

とある平面上に $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ がなす角 $\theta$ で存在するとしましょう
このとき $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ の両方に垂直で大きさが $|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|{\sin}\theta$ となるような $\overrightarrow{\mathrm{n}}$ を $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ の外積といいます

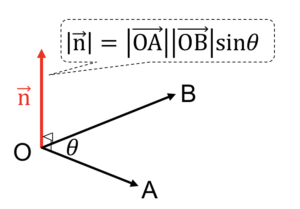
外積という名前は内積の反対のようですが、計算結果が実数だった内積と違って、外積では計算結果がベクトルになります

また上図のように $\overrightarrow{\mathrm{n}}$ として上向きのものを考える場合は

$\overrightarrow{\mathrm{n}}=\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}$

のように表現できます

一方で下図のように $\overrightarrow{\mathrm{n}}$ として下向きのものを考える場合は

$\overrightarrow{\mathrm{n}}=\overrightarrow{\mathrm{OB}}\times\overrightarrow{\mathrm{OA}}$

のように表現します

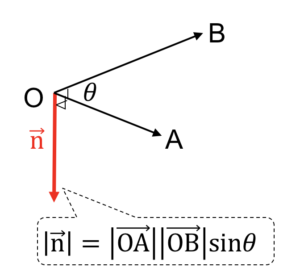
そのため、

$\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}=-\overrightarrow{\mathrm{OB}}\times\overrightarrow{\mathrm{OA}}$

の関係があります
このように $\times$ の前後に書く $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ の順番によって向きが変わるのはなぜでしょうか？
それは外積 $\overrightarrow{\mathrm{n}}(=\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}})$ の向きの定義が、 $\overrightarrow{\mathrm{OA}}$ から $\overrightarrow{\mathrm{OB}}$ へと右ねじを回したときの、つまり下図のように右手の親指を立てて青矢印の向きに親指以外を添えてみたときの、親指が指し示す向きだからです

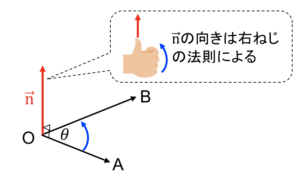
この事実は知らなくてもそこまで問題ないので難しければスルーしてもらっても大丈夫だよ！

さらにもう一つ外積で抑えておいて欲しい性質は三角形OABの面積が $\displaystyle \frac{1}{2}|\overrightarrow{\mathrm{n}}|$ で表されるということです！

なぜなら、外積の定義より $\overrightarrow{\mathrm{n}}$ の大きさは $|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|{\sin}\theta$ なので $\displaystyle \frac{1}{2}|\overrightarrow{\mathrm{n}}|=\displaystyle \frac{1}{2}|\overrightarrow{\mathrm{OA}}||\overrightarrow{\mathrm{OB}}|{\sin}\theta$ となり、これは ${\sin}{\theta}$ を用いた三角形の面積公式そのものとなるからです
「外積の大きさを $\displaystyle \frac{1}{2}$ 倍するだけで簡単に面積が求まる！」と覚えておきましょう

ここまでの解説をまとめると以下の通りです

外積の計算方法と覚え方

外積の特徴が分かったところで次は実際に $\overrightarrow{\mathrm{n}}=\overrightarrow{\mathrm{OA}}\times\overrightarrow{\mathrm{OB}}$ をどのように計算するか解説します

まず $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ が成分で与えられているとき外積 $\overrightarrow{\mathrm{n}}$ の計算結果は以下のとおりです

少しややこしくて丸暗記は厳しそうですね
そこで以下の手順で計算するのが間違いが少なくおすすめです

まず $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ の各成分を縦に２回ずつ横並びに書いて一番上と一番下の行を消します

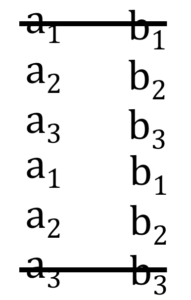
そして以下のような三色のブロックごとに分けた後、

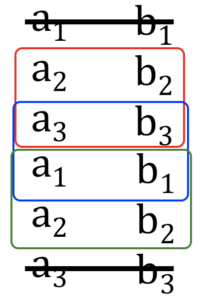
各ブロック内でたすき掛けを行い、各値を引きます

するとさきほど書いた $\overrightarrow{\mathrm{n}}$ の値が出てきました！
他のサイトでもいろいろな計算方法が書かれていましたが、この手順が一番間違いが少なく覚やすいと思います
今回の記事の応用編として、実際の入試問題での外積の活用方法や答案の書き方は以下の記事で解説しています

入試問題における外積の使い方と答案例