[latexpage]
今回は阪大オープン2018を受けたので理系数学で個人的に一番難しかった大問5(2)について解説します
(この大問5が平均点や合格最低点を大きく下げているのではないかと感じました)
模試を受けた阪大受験生の参考になれば嬉しいです
はじめの考え方
(1)で不等式を証明させられてからの(2)で極限問題なので「はさみうちかな?」と疑います
今(1)より$a_{n}>\log(n+1)$, $a_{n^2} >\log(n^2+1)$なので試しに$a_{n^2}/{a_n}$を挟んでみると
\begin{align}
\frac{\log(n^2+1)}{a_n}<\frac{a_{n^2}}{a_{n}}<\frac{a_{n^2}}{\log(n+1)} \label{1}
\end{align}
となります
この式(\ref{1})を見て思いたいのが、もし何かしらの$n$の式$g(n)$を用いて
「$\log(n+1)<a_{n}<g(n)$」と$a_{n}$を上からも挟めたら式(\ref{1})は
\begin{align}
\quad&\frac{\log(n^2+1)}{g(n)} \\
\quad&<\frac{\log(n^2+1)}{a_n} \\
\quad&<\frac{a_{n^2}}{a_{n}} \\
\quad&<\frac{a_{n^2}}{\log(n+1)} \\
\quad&<\frac{g(n^2)}{\log(n+1)}\label{2}
\end{align}
のように、うまくnの式で挟んで、はさみうちの原理に持ち込めそうだということです
そのために他に使えそうな条件はないかと問題文を見ると、まだ使用していない漸化式がありました
\begin{align}
a_{n+1}=a_{n}+\frac{1}{e^{a_n}}\label{3}
\end{align}
ただしこの漸化式は解けない漸化式です
どうすれば良いでしょうか?
ここで気づきたいのがこの漸化式が解けない漸化式になっている原因は1/$e^{a_n}$にあるということ!
もっというと$e$の肩が$a_n$じゃなく、定数や$n$の式などであれば、等差数列や階差数列なので普通に解くことが出来ますよね
つまり1/$e^{a_n}$が非常にやっかいな存在なわけです
なのでとりあえず(1)で求めた$a_{n}>\log(n+1)$を使って1/$e^{a_n}$を不等式で評価してあげると
\begin{align}
a_{n+1}= a_{n}+\frac{1}{e^{a_n}} < a_{n}+\frac{1}{n+1} \label{4}
\end{align}
となり、1/$e^{a_n}$を消すことが出来ました
(代わりに不等式になっちゃいましたがこの漸化式からたどり着きたい目標は$a_{n}<g(n)$の形であり、こちらも不等式なのでそこまで問題はなさそうです)
階差数列
さて今得ることが出来た式(\ref{4})をもう一度書き出して眺めてみましょう
\begin{align}
a_{n+1}< a_{n}+\frac{1}{n+1} \label{5}
\end{align}
式(\ref{5})を見てお気づきでしょうか!?
階差数列にそっくりであることを!
($\because$もし$<$が$=$だったら階差数列の漸化式そのもの)
ここで階差数列の解き方を復習しましょう
以下のように階差数列$a_{n+1}=a_{n}+f(n)$では$a_{n+1}-a_{n}=f(n)$として$n=1,2,\cdots, n-1$のときの式を各辺どうし全て足し合わせます
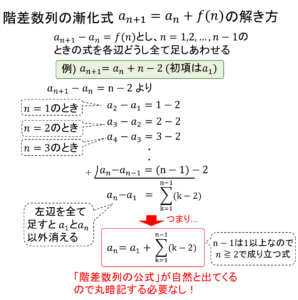
これを今回のケースでもやってみましょう
式(\ref{5})より$a_{n+1}- a_{n}<\frac{1}{n+1}$なので
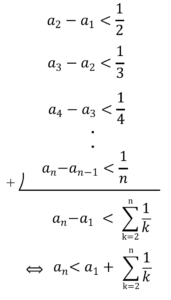
となります
さらに$a_1$が1なので
\begin{align}
a_{n}< \sum_{k=1}^{n} {\frac{1}{k}} \label{6}
\end{align}
となり目標の形$a_{n}<g(n)$にかなり近づいて来ました!
面積評価
式(\ref{6})から$a_{n}<g(n)$の形を手に入れるためには$\displaystyle \sum_{k=1}^{n} {\frac{1}{k}}<g(n)$となるような$g(n)$が見つかればよいですよね!
このように直接計算できない和から不等式を生み出したいときには面積評価が有効です
(しかも$\displaystyle \sum_{k=1}^{n} {\frac{1}{k}}$は非常に有名な形なのですぐに面積に言い換えられるようにしておきたい)
$\displaystyle \sum_{k=1}^{n} {\frac{1}{k}}$を面積に言い換えると図1, 2のように2通りの図が考えられます
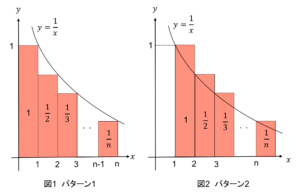
今これらの面積よりも大きい面積$g(n)$を考える必要があるので図1を採用します
(図2のようにすでにグラフから面積が飛び出した形だと、これよりも大きい面積$g(n)$が考えづらいですよね)
そして図1よりも大きくなるような面積を考えると図3のようになります
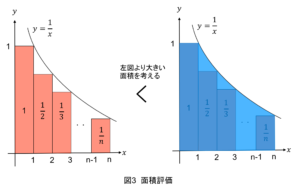
図3右側の青の面積は左側の面積より大きいですよね
(ちなみに青の面積を$0\leqq{x}\leqq1$では$y=1$としたのは、$y\leqq{1/x}$として面積が無限大となってしまうのを防ぐためです)
図3の面積をそれぞれ式になおすと
\begin{align}
\sum_{k=1}^{n} {\frac{1}{k}}<1+\int_1^n \frac{1}{x}dx=1+\log{n} \label{7}
\end{align}
となって無事$g(n)=\log{n}+1$を求めることが出来ました!
よって式(\ref{2})に$g(n)=\log{n}+1$と$g(n^2)=\log{n^2}+1$を代入すると
\begin{align}
&\frac{\log(n^2+1)}{\log{n}+1}<\frac{a_{n^2}}{a_{n}}<\frac{\log{n^2}+1}{\log(n+1)}\label{8}\\
\Leftrightarrow & \frac{\log(n^2+1)}{\log{n}+1}<\frac{a_{n^2}}{a_{n}}<\frac{2\log{n}+1}{\log(n+1)} \label{9}
\end{align}
となります
極限計算
ここからは極限の計算ですね!
左辺の分子と右辺の分母にあるlogの中の$+1$が邪魔です
($\because$もし$+1$がなければ全て$\log{n}$だけの式になる)
この$+1$を処理するのに以下の二通りの解法が考えられます
解1) $+1$をなくした不等式で挟む
$\log{n^2}<\log(n^2+1)$と$\log{n}<\log(n+1)$より式(\ref{8})は
\begin{align}
\quad&\frac{\log{n^2}}{\log{n}+1}<\frac{a_{n^2}}{a_{n}}<\frac{2\log{n}+1}{\log{n}} \label{10} \\
\Leftrightarrow \quad& \frac{2\log{n}}{\log{n}+1}<\frac{a_{n^2}}{a_{n}}<\frac{2\log{n}+1}{\log{n}}
\end{align}
と変形できますよね!
後は左辺と右辺の$n\to{\infty}$での極限が2になることからさみうちの原理を使うだけです
解2) 無理やり積の形を作る
$\log(n+1)$の中身を$n$でくくって積の形をつくると
\begin{align}
&\log(n+1)\\
=&\log{n(1+1/{n})} \nonumber \\
=& \log{n}+\log(1+1/{n})
\end{align}
となります。 $\log(n^2+1)$についても同様にすると
\begin{align}
&\log(n^2+1) \\
=&\log{n^2(1+1/{n^2})} \nonumber \\
=& \log{n^2}+\log(1+1/{n^2})\\
=&2\log{n}+\log(1+1/{n^2})
\end{align}
となるので式(\ref{8})に代入すると
\begin{align}
\quad&\frac{2\log{n}+\log(1+1/{n^2})
}{\log{n}+1} \\
\quad&<\frac{a_{n^2}}{a_{n}} \\
\quad& <\frac{2\log{n}+1}{(\log{n}+\log(1+1/{n})
)} \nonumber
\end{align}
となり、ここからは解1と同様に左辺と右辺の$n\to{\infty}$での極限が2になることからさみうちの原理を使うと良いです
長かったですが以上で無事答えまでたどり着くことが出来ました!
大問5(1)についても希望があれば解説を載せるのでコメントください