意外と知られていない数学小ネタ集

ルートの外し方
余弦定理のわな
グラフで捉える極限
差分で解く難問シグマ計算

ルートの外し方

$\sqrt{A^2}$ を $\pm{A}$ とする間違いがよくあります
そうではなく $\sqrt{A^2}$ は $A\geq{0}$ のとき $A$ 、 $A<0$ のとき $-A$ です
これを簡潔にまとめると絶対値を使って以下のようになります

$\sqrt{A^2}=|A|$

余弦定理のわな

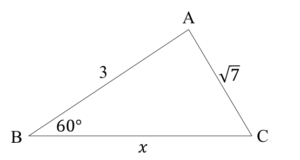
上図の $x$ の値を求めるために、三角形ABCにおいて余弦定理を用いたとします

${(\sqrt{7})^2=3^2+x^2-2\cdot3{\cdot}x{\cdot}cos60^\circ$

この2次方程式を解くと

$7=9+x^2-3x$

$x^2-3x+2=0$

$(x-1)(x-2) =0$

$x = 1, 2$

と答えが2つ出てきます
ここで正しい答えがどちらか分からなくなってしまうミスがあります
答えが2つ出てくる理由は以下の図で $x$ を求めるために余弦定理を立ててみるとわかります

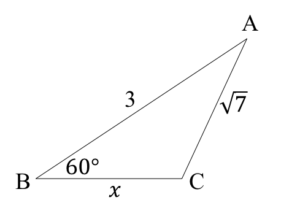
${(\sqrt{7})^2=3^2+x^2-2\cdot3{\cdot}x{\cdot}cos60^\circ$

先ほどと全く同じ式になりましたよね？
このようにはじめに立てた余弦定理の式では図が2パターン考えられるために答えも2つ出てくるんですね
なので、自分が考えているのがどちらの図なのかに合わせて $x$ の値を選択してあげる必要があります
今回でいうと、1つ目の図のほうが2つ目の図より $x$ の値が大きいので、 $x=2$ が正解です

グラフで捉える極限

以下の２つの有名な極限があります

(1) $\begin{align*} \lim_{x \to 0} \frac{e^{x}-1}{x} = 1 \end{align*}$

(2) $\begin{align*} \lim_{x \to 0} \frac{log(x+1)}{x} = 1 \end{align*}$

これは $y=e^{x}-1$ , $y=log(x+1)$ , $y=x$ の３つのグラフを図示すると即座に理解できます！

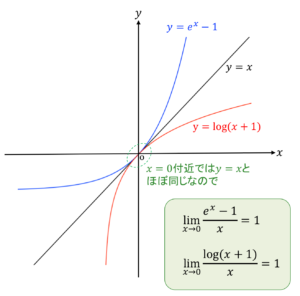
図より $x=0$ 付近では $y=e^{x}-1$ と $y=log(x+1)$ は $y=x$ のグラフとほぼ一致してますよね
つまり $\frac{e^{x}-1}{x}$ や $\frac{log(x+1)}{x}$ の分母と分子が $x$ の値が0に近づいた際にほとんど同じ値をとるので極限値は1となります

また別の捉え方として式(1)は「 $e^x$ の原点での微分係数は1」であること、式(2)は「 $e$ の定義、つまり $\lim_{x \to 0} (1+x)^\frac{1}{x} = e$ 」を考えても分かります

差分で解く難問シグマ計算

以下のシグマ計算の問題を考えてみてください

$\sum_{k=1}^{n} k{\cdot}k ! = ?$

見たことがない形で以外に難しいのではないでしょうか？
シグマ計算は公式を用いて計算するのに慣れているかもしれませんが、部分分数分解の問題のように差分の形を作りだすと値が次々と消えていき、答えを出せることがあります

今回の問題では $k{\cdot}k!$ を $(k+1-1)\cdot{k!}=(k+1)!-k!$ と差分の形にしてあげることで以下のように真ん中の値が次々と消えていきます

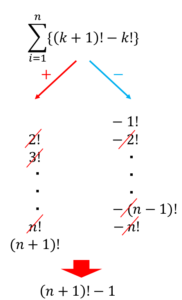
シグマ計算で差分の形を作り出したときは上図のように縦に書き出すと消えるのがわかりやすいよ♪

以上より計算結果は(n+1)!-1なります
これを式で表すと以下の通りです

(3) $\begin{align*} \sum_{k=1}^{n} k{\cdot}k ! &=\sum_{k=1}^{n} \{(k+1-1)\cdot{k!}\} \\ &=\sum_{k=1}^{n} \{(k+1)!-k!\} \\ &=(n+1)!-1 \end{align*}$

差分の形は非常に重要で、有名公式も $\sum_{k=1}^{n} k^2 = \frac{1}{6}n(n+1)(2n+1)$ も実は差分を用いて導出出来ます
余裕のある方は考えてみてください！