「三角形ABCの重心,内心,外心,垂心のどれか2つが一致する」と言われたら、三角形ABCは正三角形です
どの2つが来ても図形的に証明出来るのが理想ですが、特に重心と外心が一致するときはベクトルで簡単に証明可能なので知っておくのがおすすめです
なので今回は重心と外心が一致するとき正三角形であることをベクトルで証明します
今回のポイント
今回抑えて欲しい内容は以下の通りです
- 重心と外心が一致するとき正三角形であることをベクトルで証明できるようにする
証明
三角形ABCの外心をO, 重心をGとすると以下の式が成り立ちます
\[\left|\overrightarrow{\mathrm{OA}}\right|=\left|\overrightarrow{\mathrm{OB}}\right|=\left|\overrightarrow{\mathrm{OC}}\right|
\]
\[\overrightarrow{\mathrm{OG}}=\displaystyle\frac{\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}}{3} \]
ここで外心と重心が一致するとき、つまりO=Gのとき\(\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{0}}\)なので
\begin{align}
&{\left|\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}\right|}^2={\left|-\overrightarrow{\mathrm{OC}}\right|}^2\nonumber \\
\quad\Leftrightarrow& {\left|\overrightarrow{\mathrm{OA}}\right|}^2+{\left|\overrightarrow{\mathrm{OB}}\right|}^2+2\overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}={\left|\overrightarrow{\mathrm{OC}}\right|}^2\nonumber \\
\quad\Leftrightarrow& \overrightarrow{\mathrm{OA}}\cdot\overrightarrow{\mathrm{OB}}=-\frac{1}{2}{\left|\overrightarrow{\mathrm{OA}}\right|}^2\nonumber \\
\quad\Leftrightarrow& \cos{\angle\mathrm{AOB}}=-\frac{1}{2}\nonumber
\end{align}
となります
よって\(\angle\mathrm{AOB}=120^\circ\)なので円周角と中心角の関係から\(\angle\mathrm{ACB}=60^\circ\)と分かります
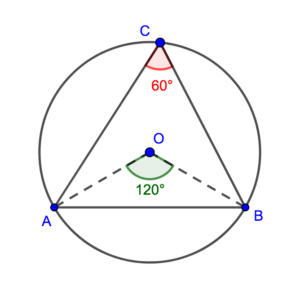
同様にして\(\angle\mathrm{CBA}=60^\circ\), \(\angle\mathrm{BAC}=60^\circ\)なので三角形ABCは正三角形であるといえます
以上で無事証明出来ました!