今回のポイント
今回抑えて欲しい内容は以下の通りです
- 正射影ベクトルとはなにかを知る
- 正射影ベクトルの公式を証明も抑えた上で暗記する(丸暗記しない!)
正射影ベクトルは必須ではないもののしっておくと便利な公式です
黄チャート数ⅡBp385にも載っていましたが、証明の部分で場合分けが発生していて少しややこしかったので、この記事では場合分けをせずに証明する方法もお伝えします
正射影ベクトル
まずは以下の図をみてください
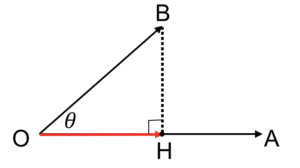
\(\overrightarrow{\mathrm{OA}}\)と\(\overrightarrow{\mathrm{OB}}\)がある中で、点Bから直線OAへと降ろした垂足をHとしています
このとき\(\overrightarrow{\mathrm{OH}}\)は\(\overrightarrow{\mathrm{OB}}\)の\(\overrightarrow{\mathrm{OA}}\)への正射影ベクトルといい、式で表すと以下のようになります
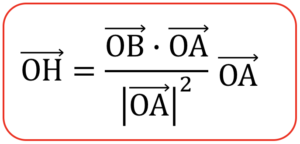
この式の意味は「\(\overrightarrow{\mathrm{OH}}\)が\(\overrightarrow{\mathrm{OA}}\)の実数倍なのは図からも明らかだけど実はその係数は(\(\overrightarrow{\mathrm{OB}}\)と\(\overrightarrow{\mathrm{OA}}\)の内積)/(\(\overrightarrow{\mathrm{OA}}\)の大きさの二乗)で表せるよ!」ということです
そう考えると少し覚えやすいのではないかと思います
また両辺に絶対値をとって\(\overrightarrow{\mathrm{OH}}\)の大きさを考えると以下のようになります
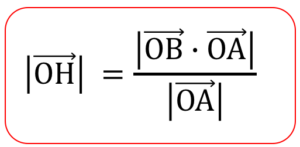
補足
正射影ベクトルの名前の由来を簡単に説明します
正射影とは「スクリーンに垂直な光線が当たって出来る影」のことです
今回の図でいうと、もし\(\overrightarrow{\mathrm{OA}}\)にスクリーン、\(\overrightarrow{\mathrm{OB}}\)に壁があり、上側から垂直な光線が入ってきたとすると、\(\overrightarrow{\mathrm{OH}}\)の部分に影ができますよね?
そのため\(\overrightarrow{\mathrm{OH}}\)を正射影ベクトルといいます
正射影ベクトルの公式の証明
正射影ベクトルの公式の証明では図より明らかな事実として「\(\overrightarrow{\mathrm{OH}}\)が\(\overrightarrow{\mathrm{OA}}\)の実数倍であること」と「\(\overrightarrow{\mathrm{BH}}\)と\(\overrightarrow{\mathrm{OA}}\)が垂直であること」を用います
その証明はこちらです

正射影ベクトルを公式として入試で使って良いか不安な方は、この証明の手順と同じことをすれば良いでしょう
正射影ベクトルの使い所
正射影ベクトルを知っていると役立つケースは入試問題でも多数存在します
特におすすめの使い方は以下の記事で解説しているのでぜひそちらもよんでみてください!
丸暗記している人が多い「点と直線の距離の公式」を簡単に導けたり、入試でよく問われる「正四面体の体積」を一瞬で求められるようになります!