今回のポイント
今回抑えて欲しい内容は以下の通りです
- 正射影ベクトルを使って点と直線の距離の公式を証明できるようにする
では説明していきます！
正射影ベクトル
復習になりますが正射影ベクトルは以下の通りです
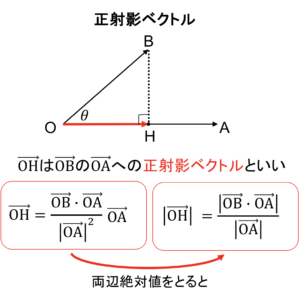少し怪しい方は以下の記事を読んでもらうと理解が深まると思います
点と直線の距離の公式とその証明
まず点と直線の距離の公式はこちらです
覚えてはいても証明は出来ない人が多い公式の一つです
では証明していきましょう
まず直線 \(\mathrm{a}x+\mathrm{b}y+\mathrm{c}=0\)上のある点Bの座標を\((\mathrm{x_0},\mathrm{y_0})\)とすると
\[\mathrm{ax_0}+\mathrm{by_0}+\mathrm{c}=0\]
がえられます
次に直線\(\mathrm{a}x+\mathrm{b}y+\mathrm{c}=0\)の法線ベクトルを\(\vec{\mathrm{n}}\)とすると\(\vec{\mathrm{n}}=(\mathrm{a},\mathrm{b})\)となります(詳しくは「法線ベクトルの記事」参照)
ここで\(\overrightarrow{\mathrm{AH}}\)は\(\overrightarrow{\mathrm{AB}}\)の\(\overrightarrow{\mathrm{n}}\)への正射影ベクトルであることから
が成り立つので、\(\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\)とした後に各ベクトルに成分を代入して計算していくと
となります
ここで\(\mathrm{ax_0}+\mathrm{by_0}+\mathrm{c}=0\)であったことを思い出すと、\(\mathrm{ax_0}+\mathrm{by_0}=-\mathrm{c}\)となるので
と変形できます
よく見るとこれは点と直線の距離の公式そのものですよね！
このように正射影ベクトルを用いると非常に簡潔に点と直線の距離が証明出来るのでぜひ覚えておくようにしましょう！