以前、反転(軌跡)の定義と性質について動画で解説しました(詳しくは「反転の性質」参照)
実はその反転の性質をフル活用すると、入試問題であっても瞬時に軌跡の方程式を算出可能です！
今回は実際に大阪市立と横浜市立大医学部医学科で出題された入試問題で、その方法についてわかりやすく解説していきます
今回のポイント
今回抑えて欲しい内容は以下の通りです
- 反転の入試問題を瞬時に解く方法を知る
また前回解説した反転の定義や性質は全て抑えているものとして解説していくので、不安なかたはまず以下の記事をみていただけると嬉しいです
大阪市立大の過去問
まずは以下の問題をみてください
過去に文理共通で出題された大阪市立大の入試問題です
条件が反転の定義そのものなので点Qは点Pを中心O、半径2の反転円によって反転させた点であることがわかりますね！
ひとまず反転円と点Pが動く直線\(x=1\)を図示してみましょう
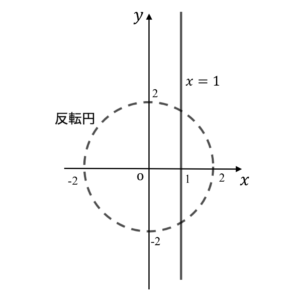ここで直線x=1は原点Oを通らない直線なので反転の性質②「点Pが反転円の中心Oを通らない直線上を動くとき、点QはOを通る円上を動く」に対応します
あとはその円が原点O以外に通る点がわかれば図示できそうですね！
そのためには点Pがx軸またはy軸上に存在するときに注目すると良いです
つまり今回の問題でいうと点Pがx軸上の点(1,0)にいるときに注目します
このときOP=1なので、点QはOを端点とする半直線OP上かつ「OP・OQ=4」を満たすことからQ(4, 0)と分かりますね
最後に点Pの軌跡にはx軸に関して対称性があることに注意すると求める点Qの軌跡は下図の赤線のように「中心(2, 0)、半径2の円になる」ことが分かります
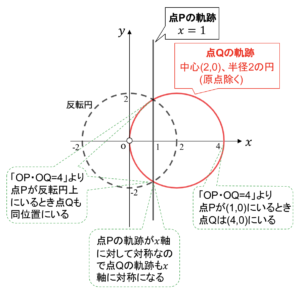
ただし性質の解説でも述べたように点Qは原点は通りません
また反転円と点Pの軌跡(今回は直線\(x=1\))に交点が存在するときは点Qの軌跡もその交点を通ることにも気をつけましょう
(そもそも交点が存在しないときは気にしなくて良いです)
横浜市立大医学部医学科の過去問
次に横浜市立大医学部医学科で出題された入試問題です
さきほどの大阪市大の問題と同じく、条件が反転の定義そのものなので点Qは点Pを中心O、半径2の反転円によって反転させた点であることがわかりますね
そして曲線\((x-2)^2+(y-3)^2=13\)は原点Oを通る円なので反転の性質③「点Pが反転円の中心Oを通る円上を動くとき、点QはOを通らない直線上を動く」に対応します
そして反転円と点Pの軌跡に交点が存在するときは点Qの軌跡もその交点を通ることに気をつけて、これらを図示すると以下のようになります
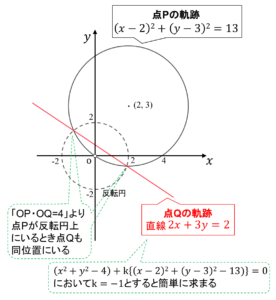
このように反転の性質を利用すると瞬時に軌跡を求めることが出来ました！
問題によっては点Qの正確な軌跡(=軌跡の方程式)を求めることは難しいかもしれませんが、反転の性質４つを抑えておくだけで、おおまかな軌跡は知ることができます
ただし反転の性質を答案で用いてよいかは微妙なところなので、普通の解き方は問題集などでしっかりマスターしておき、最後の検算用に性質を活用するのが良いかと思います
ちなみに数Ⅲ複素数の単元や難関大の入試問題には，反転であることが一見わかりにくい問題が存在します
また希望があれば近い内に解説するのでコメントで教えてくださると嬉しいです