定積分関数の多くの問題では以下のように関数を求めるように言ってきます
- \(f(x)=1+2\displaystyle \int_0^1 {(xt+1)f(t)}dt\)を満たす関数\(f(x)\)を求めよ。
こういった問題では,定積分関数を3パターンに分類し,各パターンごとの解き方を抑えておくことが大切です
今回はそんな定積分関数の問題について具体的に解説します!
今回のポイント
今回抑えて欲しい内容は以下の通りです
- 定積分関数を3パターンに分類し,それぞれの解法を言えるようにする
- 問題を見てどのパターンか判断できるようにする
では説明していきます!
定積分関数の解法3パターン
定積分関数とは\(\displaystyle g(x)=\int_2^x {f(t)} dt\)のように定積分を含んだ関数のことです
以下の3パターンに分類することができ,それぞれの特徴に応じて解き方が決まってきます!
パターン①: 積分区間が定数のみ
パターンの1つ目は積分区間が定数のみの定積分関数です
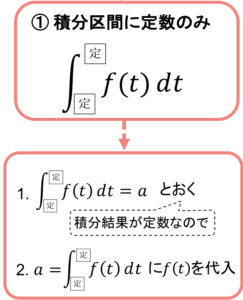
積分区間が定数のみということは定積分関数の計算結果は定数なので,まずは定積分関数を「=a(定数)」とおきます
そしてa=(定積分関数)に\(f(t)\)を代入して解いていきます
(後ほど具体的な問題で解説します)
パターン②: 積分区間に変数xを含む
パターンの2つ目は積分区間に変数xを含む定積分関数です
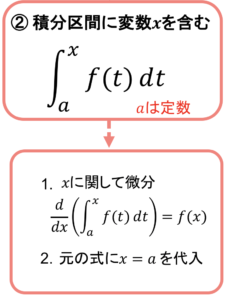
この場合,定積分関数の計算結果はxの式となります
ここで\(\displaystyle g(x)=\int_a^x {f(t)} dt\)を微分すると,\(f(x)\)そのものが出てくるので,まずはxに関して微分します
次にx=aのとき定積分関数の計算結果が0になることを利用して解いていきます
(後ほど具体的な問題で解説します)
パターン③: 積分する関数がxとtの式
パターンの3つ目は積分する関数がxとtの式の定積分関数です

上図のように,定積分関数がtに関する積分の場合,xは積分には関係ないので,まずは外に出します
そうすると,さきほどのパターン①or②の形に必ず帰着できるので,それぞれの解き方に従って解いていきます
これだけだと分かりづらいと思うので具体的な問題で3パターンの解き方を確認しましょう!
問題1
\(f(x)=x^2+\displaystyle \int_0^1 {tf(t)}dt\)を満たす関数\(f(x)\)を求めよ。
問題1の解答
問題1は積分区間が定数のみなのでパターン①ですね!
なのでまずは
\(\displaystyle\int_0^1 {tf(t)} dt=a\)(定数)
とおくと
\(f(x)=x^2+a\)
となります
次に\(a=\displaystyle\int_0^1 {tf(t)} dt\)に\(f(t)=t^2+a\)を代入すると
\begin{align}
a&=\int_0^1 {t(t^2+a)} dt\\
&=\left[\frac{1}{4}t^4+\frac{a}{2}t^2\right]^1_0=\frac{1}{4}+\frac{a}{2} \nonumber
\end{align}
となるので\(a=\displaystyle\frac{1}{2}\)と分かり
\(f(x)=x^2+\displaystyle\frac{1}{2}\)
となります
問題2
\(\displaystyle \int_a^x {f(t)}dt=x^2-3x+2\)を満たす\(f(x)\)と\(a\)を求めよ。
問題2の解答
今回は積分区間に変数xを含むのでパターン②ですね!
なのでまずは与式の両辺をxで微分すると
\(\displaystyle\frac{d}{dx} \int_a^x {f(t)}dt=2x-3\)
となります
ここで\(\displaystyle\frac{d}{dx} \int_a^x {f(t)}dt=f(x)\)なので
\(f(x)=2x-3\)
と分かりますね!
そして与式に\(x=a\)を代入すると
\(\displaystyle\int_a^a {f(t)}dt=a^2-3a+2\)
ですね!
ここで\(\displaystyle\int_a^a {f(t)}dt=0\)なので\((a-2)(a-1)=0\)を解いて
\(a=1, 2\)
となります
問題3
\(f(x)=1+2\displaystyle \int_0^1 (xt+1)f(t)dt\)を満たす関数\(f(x)\)を求めよ。
問題3の解答
今回は積分する関数がxとtの式なのでパターン③ですね!
なのでxを\(\int\)の外に出すと
\(f(x)=1+2x\displaystyle \int_0^1 {tf(t)}dt+2\displaystyle \int_0^1 {f(t)}dt\)
となります
すると定積分関数の積分区間が定数のみになったのでパターン①に帰着できますね!
よって
\(\displaystyle \int_0^1 {tf(t)}dt=a, \displaystyle \int_0^1 {f(t)}dt=b\)
とおくと
\(f(x)=2ax+2b+1\)
です
よって\(a=\displaystyle\int_0^1 {t(2at+2b+1)} dt\)を計算すると
\(2a-6b-3=0\cdots(1)\)
となり,同様に\(b=\displaystyle\int_0^1 {2at+2b+1} dt\)を計算すると
\(a+b+1=0\cdots(2)\)
になります
よって式(1)(2)より\(\displaystyle a=-\frac{3}{8}, b=-\frac{5}{8}\)と分かるので
\(\displaystyle f(x)=-\frac{3}{4}x-\frac{1}{4}\)
となります
以上が各パターンごとの問題での解き方です
ちなみにパターン②では問題2以外にも,極値をとるときのxの値や最大値などを聞いてくる問題もありますが,まずはここで挙げた解き方を覚えておくのが大切です!
頑張って抑えておくようにしましょう〜