入試問題の頻出単元の1つに反転があります
青チャート(数Ⅱ軌跡と方程式)でも登場し理解が難しい単元として有名ですが、実は動画で視覚的に捉えると非常に分かりやすくなります
なので今回はそんな反転の性質について動画を用いて解説していきます
目次
今回のポイント
今回抑えて欲しい内容は以下の通りです
- 反転の定義を正しく言えるようにする
- 反転の4つの性質を視覚的に押さえる
では説明していきます!
反転とは?
まず原点Oを中心とする半径\(r\)の円(反転円と呼ぶ)があるとします
このとき原点Oと異なる点Pを、Oを始点とする半直線OP上にあり「OP・OQ=r2」を満たす点Qに移すことを「点Pから点Qへの(反転円による)反転」と呼びます
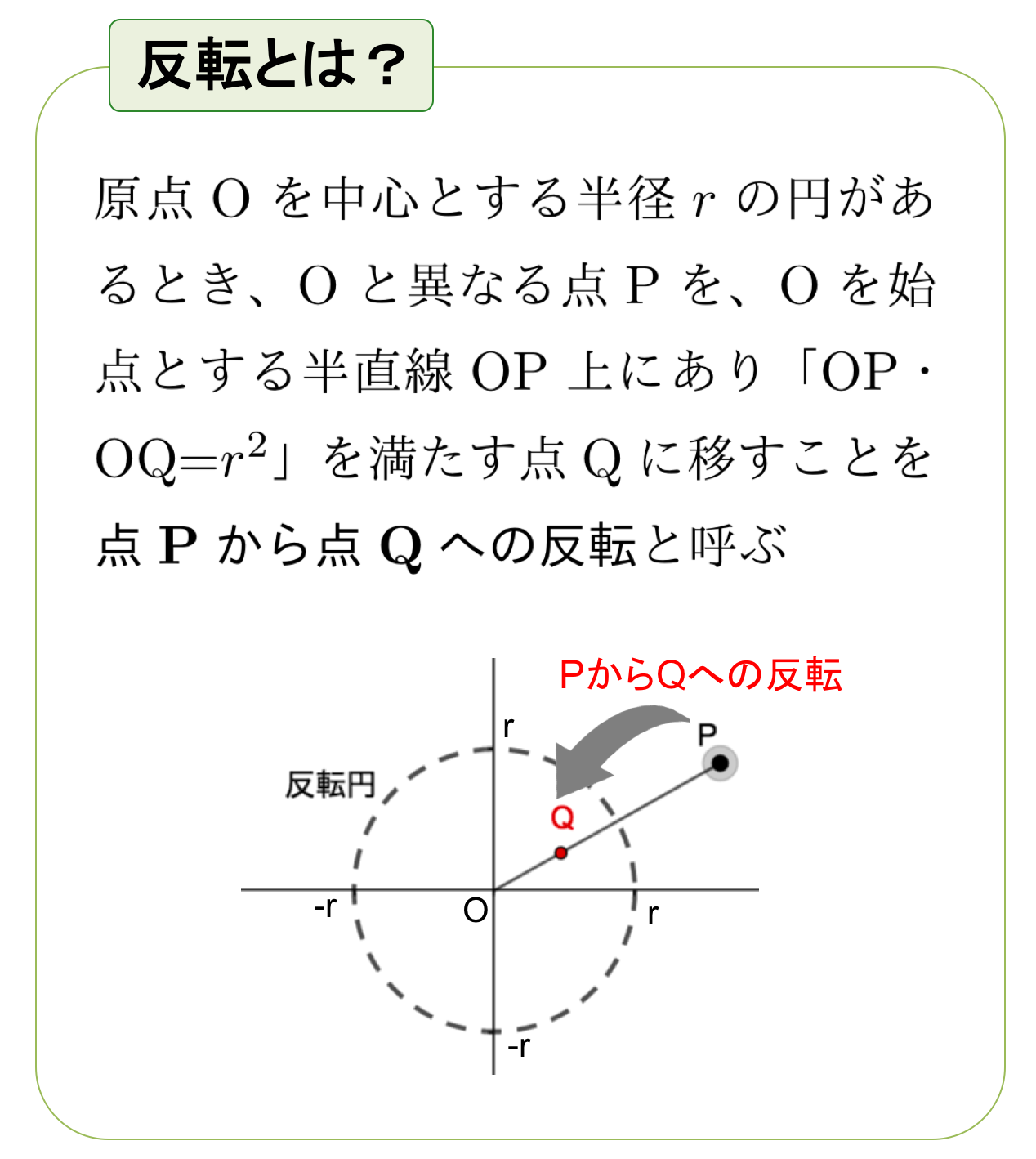
反転と呼ぶのは、以下の動画のように、点Pがどのような位置にあったとしても、点Qが反転円に関して点Pと反転したような位置、つまり点Pが反転円の外側にあるとき点Qは内側、点Pが内側にあるとき点Qは外側、に存在するためです

そして入試問題では点Pが決まった図形上を動く(=ある軌跡を描く)ときに点Qはどのような動きをするのか(=どのような軌跡を描くのか)問われます
そこで大切なのは以下のような反転の4つの性質を抑えておくことです

この反転の性質を正しく抑えておくと、後は点Qが明らかに通る点を何点か見つけるだけで、点Qの軌跡を把握可能になります!
なのでまずは反転の性質を1つずつ動画で見ていき正しく抑えましょう!
反転の性質①「原点を通る直線→原点を通る直線(自分自身)」
性質の1つ目は
「点Pが反転円の中心Oを通る直線上を動くとき、点Qも同じ直線上を動く」
です
 動画を見ると、点Pが反転円(半径r=1)の中心Oを通る直線上を動くとき、点Qも同じ直線上を動いているのが分かると思います
動画を見ると、点Pが反転円(半径r=1)の中心Oを通る直線上を動くとき、点Qも同じ直線上を動いているのが分かると思います
点Qは半直線OP上かつ「OP・OQ=r2」を満たす点なので、点Pが原点に近づく(=OPの長さが0に近づく)ほど点Qは半直線OP上を駆け上がっていく(=OQの長さが無限大に近づく)ことになります
また点Pと点Qは原点は通らないことに注意してください
そもそも点Pは反転の定義より原点Oとは異なる点なのでOP\(\neq\)0ですよね?
よって「OP・OQ=r2」からOQ\(\neq\)0となり点Qも原点Oと一致することはないためです
(動画では点Pは原点を通っているようにみえるかもしれませんが、限りなく0に近い値を正から負へ変化させただけです)
これは反転の性質①〜④に共通の性質なので覚えておきましょう!
反転の性質②「原点を通らない直線→原点を通る円」
性質の2つ目は
「点Pが反転円の中心Oを通らない直線上を動くとき、点QはOを通る円上を動く」
です
 動画を見ると、点Pが反転円の中心Oを通らない直線上(動画では\(x=1\))を動くとき、点QはOを通る円上を動くのが分かると思います
動画を見ると、点Pが反転円の中心Oを通らない直線上(動画では\(x=1\))を動くとき、点QはOを通る円上を動くのが分かると思います
また点Pが反転円上を通る(OP=rである)場合は点Qも同じ位置にいるのは「OP・OQ=r2」を考えると当然ですね
性質①で述べたように、点Qは原点Oは通らない点にも注意しましょう
反転の性質③「原点を通る円→原点を通らない直線」
性質の3つ目は
「点Pが反転円の中心Oを通る円上を動くとき、点QはOを通らない直線上を動く」
です
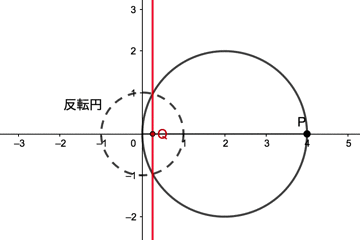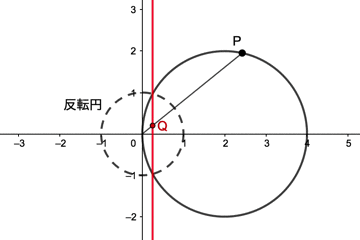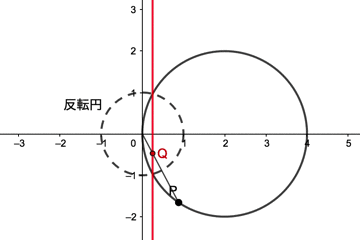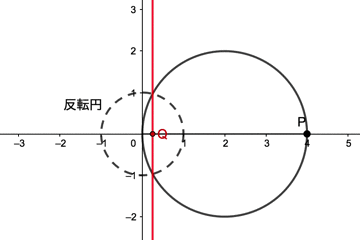
動画を見ると、点Pが反転円の中心Oを通る円(中心(2,0)で半径2の円)上を動くとき、点QはOを通らない直線上を動くのが分かると思います
「OP・OQ=r2」より点Pが反転円上を通る場合は点Qも同じ位置にいるので、点Qが描く直線は点Pが描く円と反転円の交点を通ることになります
反転の性質④「原点を通らない円→原点を通らない円」
ラストである性質の4つ目は
「点Pが反転円の中心Oを通らない円上を動くとき、点QはOを通らない円上を動く」
です
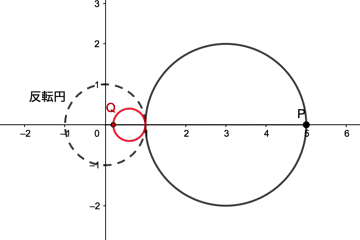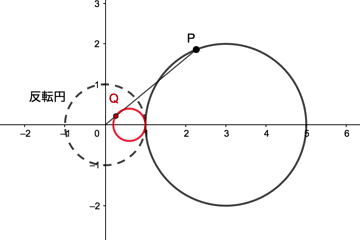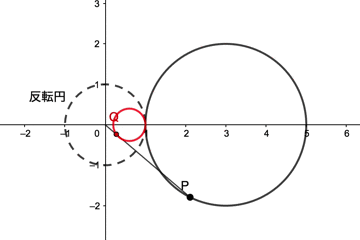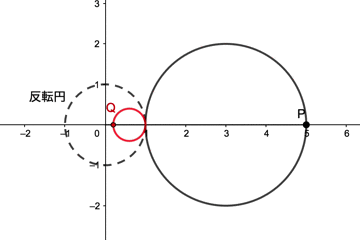 動画を見ると、点Pが反転円の中心Oを通らない円(中心(3,0)で半径2の円)上を動くとき、点QはOを通らない円を動くことが分かると思います
動画を見ると、点Pが反転円の中心Oを通らない円(中心(3,0)で半径2の円)上を動くとき、点QはOを通らない円を動くことが分かると思います
このように動画で捉えると反転の性質①〜④への理解が深まったのではないでしょうか?
よく参考書では各性質の証明を中心に扱っていますが、証明よりも性質を正しく抑えておくことがはるかに大切です
なぜなら反転の性質をフル活用すると、入試問題であっても瞬時に軌跡の方程式を算出可能だからです!
その方法については以下の記事で実際の入試問題を例に挙げて詳しく解説しているのでよかったらみてください!